- euclidien
-
euclidien, ienne [ øklidjɛ̃, jɛn ] adj.• v. 1730; de Euclide, mathématicien gr.♦ Math. Relatif à Euclide et à ses postulats. Algorithme, anneau, espace euclidien. Géométrie euclidienne, issue des travaux d'Euclide et généralisée par la suite aux espaces de dimension infinie. ⊗ CONTR. Non-euclidien.
● euclidien, euclidienne adjectif Relatif à Euclide ou à ses travaux. ● euclidien, euclidienne (expressions) adjectif Espace euclidien, espace ponctuel affine muni d'une métrique euclidienne, associé à un espace vectoriel euclidien. Géométrie euclidienne, géométrie qui repose sur les cinq demandes ou postulats d'Euclide. (Quand on remplace le 5e postulat par un autre, on obtient les géométries non-euclidiennes.) Espace vectoriel euclidien, espace vectoriel préhilbertien réel de dimension finie. Norme euclidienne, norme définie sur un espace vectoriel euclidien E de dimension finie n par :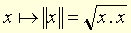
où x.x = f(x,x) est le carré scalaire de x, f étant une forme bilinéaire symétrique non dégénérée positive. (Dans une base orthogonale relativement à f, on a : 
.)
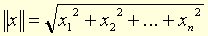euclidien, enneadj. GEOM Relatif à la géométrie d'Euclide, qui admet le postulat des parallèles (par oppos. aux géométries non euclidiennes).|| Qui traite des problèmes d'angles et de distance (par oppos. à la géométrie affine).⇒EUCLIDIEN, IENNE, adj.[En parlant d'une géométrie, d'un être géométrique] Fondé sur le postulat d'Euclide selon lequel deux parallèles ne se rencontrent jamais. Droite, géométrie euclidienne. Si l'on se donne l'espace euclidien, il est impossible de construire une figure fermée avec deux lignes droites. Avec l'espace de Riemann, c'est possible (RUYER, Esq. philos. struct., 1930, p. 344).♦ Non (-)euclidien. Qui n'est pas fondé sur le postulat d'Euclide. Les monstres non-euclidiens, comme l'espace courbe et les parallèles qui se rencontrent (ALAIN, Propos, 1922, p. 391). La géométrie classique d'Euclide ou les géométries non euclidiennes de Lobatchefsky et de Riemann (Gds cour. pensée math., 1948, p. 256).— Rare. [En parlant d'une pers.] Partisan de la géométrie d'Euclide. Géomètre euclidien. Cf. atomistique ex. 2 :• Comment cesserais-je d'être euclidien si je n'arrive pas à être euclidien, j'entends être euclidien comme on est catholique? J'en suis toujours à admirer que la somme des angles d'un triangle soit égale à deux droits.ALAIN, Propos, 1924, p. 607.♦ Non-euclidien. Qui n'est pas partisan de la géométrie d'Euclide. Géomètre non-euclidien (POINCARÉ, Valeur sc., 1905, p. 62).Prononc. :[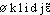
], fém. [-
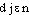]. Étymol. et Hist. Av. 1745 (Desfontaines, s. réf. ds Trév. 1752). Dér. de Euclide, nom du mathématicien gr. du IIIe s. av. J.-C.; suff. -ien. En angl. euclidean dès 1660 ds NED. Fréq. abs. littér. :80.euclidien, ienne [øklidjɛ̃, jɛn] adj.❖♦ Relatif à Euclide. || Méthode euclidienne d'exposition de la géométrie. N. || Un, une euclidien(ne) : partisan ou praticien de la géométrie d'Euclide. || Les euclidiens et les non-euclidiens.1 (…) je suis fâché que vous désigniez par le nom de Newtoniens ceux qui ont reconnu la vérité des découvertes de Newton : c'est comme si on appelait les géomètres Euclidiens.Voltaire, Lettre à Clairant, 1650, 19 août 1759.2 (…) Luneburg a cru pouvoir établir que l'espace perceptif élémentaire était riemannien et non pas euclidien (perception des parallèles, etc.), ce qui est peut-être exagéré, mais semble montrer tout au moins l'existence d'une situation indifférenciée à partir de laquelle les structures euclidiennes ne s'organisent que secondairement.J. Piaget, Épistémologie des sciences de l'homme, p. 368.♦ Géométrie euclidienne : géométrie à trois dimensions fondée sur le postulatum d'Euclide : « Par un point extérieur à une droite, on ne peut mener qu'une seule parallèle à cette droite ». ⇒ Espace (cit. 9 et supra), géométrie. || Géométries non euclidiennes.❖COMP. Non euclidien.
Encyclopédie Universelle. 2012.
